date: 03.21.2025
homotopy groups of spheres are ALL FINITE except for \(\pi_n(S^n)\) and \(\pi_{4k-1}(S^{2k})\), both of which also include a copy of \(\mathbb{Z}\).
Serre's original 1953 paper is entitled Groupes D'Homotopie Et Classes De Groupes Abéliens. I do not know a freely accessible English version. You can also read about this theorem in Hatcher's Spectral Sequences chapter, under the subsection Rational Homotopy Groups.
In this talk, I first compute the rational homotopy groups of spheres to be zero except, in the appropriate degrees, \(\mathbb{Q}\). After, I conclude finite generation of the torsion part using Serre's theory of classes of abelian groups. I assume that you know about the Serre spectral sequence, and in these notes I draw the relevant ones and work out all the details carefully.
For an \((k-1)\)-connected space \(X\), consider the fibration $$F \hookrightarrow X \rightarrow K(\pi_k(X),k).$$ Notice that by the long exact sequence of homotopy groups, \(F\) is \(k-\)connected and has higher homotopy groups agreeing with those of \(X\). (By definition, \(F\) is the next stage of the Whitehead tower.)
To find \(\pi_{k+1}(X),\) it then suffices to find \(\pi_{k+1}(F)\); since \(F\) is \(k-\)connected, this is the same, by Hurewicz, as \(H_{k+1}(X)\). But this is computable: we can use the Serre spectral sequence to compute it if we know the cohomology of \(X\) and of \(K(\pi_k(X),k).\)
One caveat: Hurewicz only works for integer coefficients. But we can get around this relatively easily:
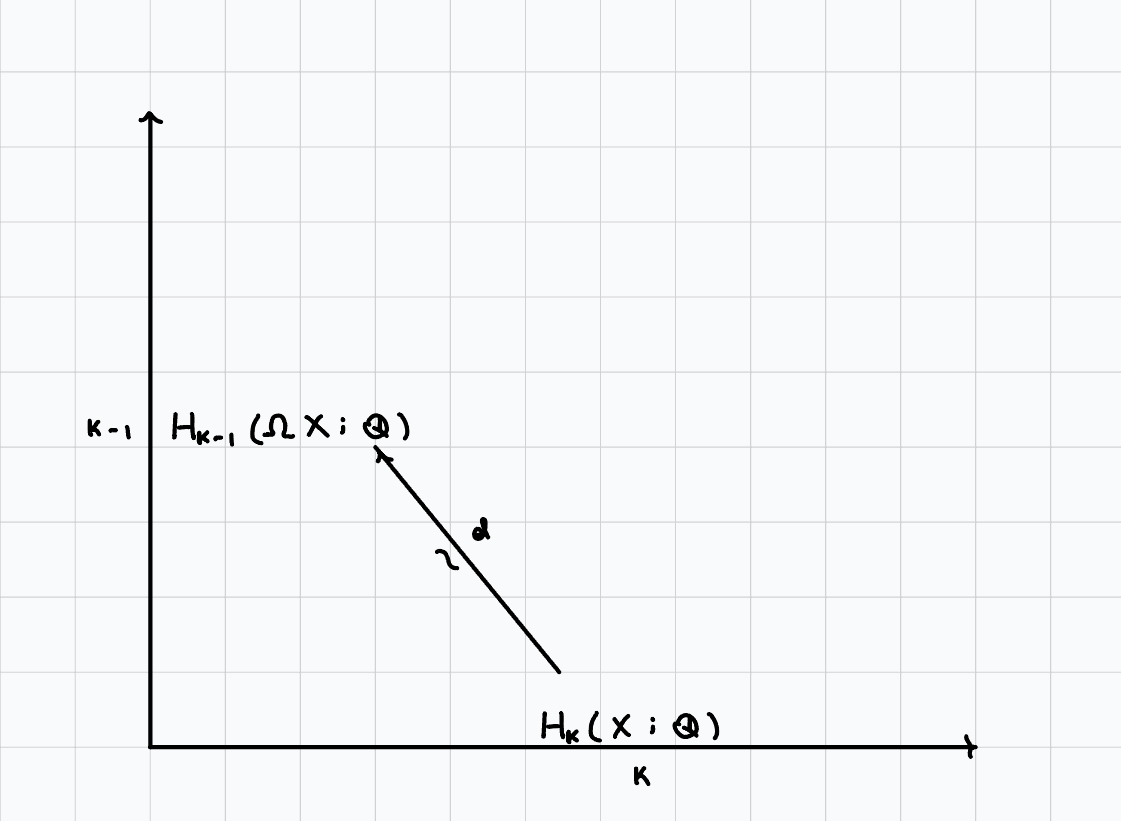
Proposition. If \(\pi_i(X) \otimes \mathbb{Q} = 0\) for \(i < k\), then \(\pi_k(X) \otimes \mathbb{Q} = H_i(X;\mathbb{Q})\).
 Everything in positive degree must die by the \(E^{\infty}\)-page, so the differential forces the desired isomorphism.
The base case for the induction comes from $$\pi_2(X) = \pi_1(\Omega X) = \pi_1(\Omega X)^{\text{ab}} = H_1(\Omega X; \mathbb{Z})$$
since a \(\pi_2\) is already abelian, and then applying universal coefficients.
Everything in positive degree must die by the \(E^{\infty}\)-page, so the differential forces the desired isomorphism.
The base case for the induction comes from $$\pi_2(X) = \pi_1(\Omega X) = \pi_1(\Omega X)^{\text{ab}} = H_1(\Omega X; \mathbb{Z})$$
since a \(\pi_2\) is already abelian, and then applying universal coefficients.
Our goal is to compute the rational homotopy groups of \(X=S^n\), whose cohomology we already know, and we also know that \(\pi_n(S^n) = \mathbb{Z}\). Let us now compute the rational cohomology of \(K(\mathbb{Z},n)\).
We will prove the following: $$H^*(K(\mathbb{Z},n); \mathbb{Q}) = \begin{cases} \mathbb{Q}[\iota_n] & n \text{ even} \\ \mathbb{Q}[\iota_n]/(\iota_n^2) & n \text{ odd.} \end{cases}$$ by inducting on \(n\). (The generator is in degree \(n\) for both cases.)
Sanity checks.
The induction will use the path-loop fibration for \(K(\mathbb{Z},k)\): $$ K(\mathbb{Z},n-1) = \Omega K(\mathbb{Z},n) \hookrightarrow PK(\mathbb{Z},n) \rightarrow K(\mathbb{Z},n)$$ to which we apply the Serre spectral sequence. The path space \(PK(\mathbb{Z},n)\) is contractible, so the \(E_{\infty}\)-page should be \(0\) everywhere for positive degree.
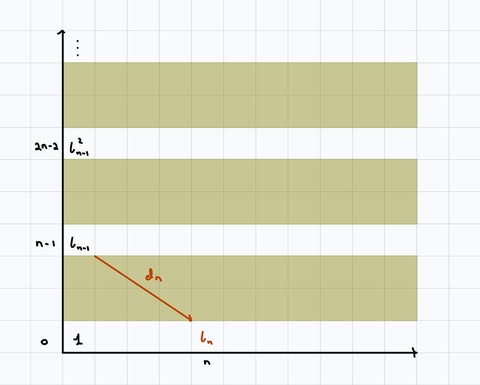
Inductively, we know that for the fiber, \(H^*(K(\mathbb{Z},n-1); \mathbb{Q}) = \mathbb{Q}[\iota_{n-1}],\) so on the \(E_2\)-page, we know the \(0\)-th column and also that it has to be \(0\) except rows whose degrees are multiples of \(n-1\).
In the \(E_\infty\)-page, the generator \(\iota_{n-1}\) must be killed. The only differential that could kill it is \(d_n\), so there must be a generator in the base in degree \(n\) which \(d_n\) maps to.
This new generator causes there to be \(\iota_{n-1}^k\iota_n\) terms. Fortunately, by the Leibniz rule, inductively we have \(d_n(\iota_{n-1}^{k+1}) = k \cdot \iota^{k}_{n-1} \iota_n\). Since \(k\) is invertible in \(\mathbb{Q}\), this kills \(\iota_{n-1}^{k+1}\). Further, notice that \(\iota_n^2=0\), since \(d_n \circ d_n(\iota_{n-1}^2) = d_n(\iota_{n-1}\iota_n) = \iota_n^2\) but \(d_n \circ d_n = 0.\) So \(\iota_{n-1}^k\iota_n\) is also killed.
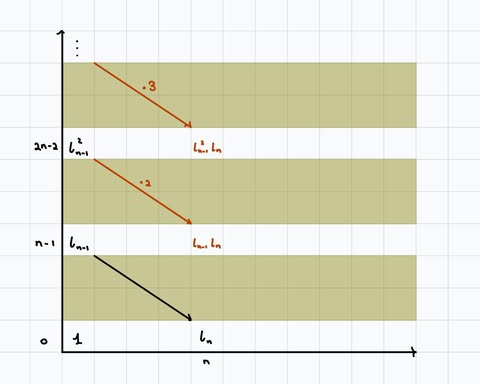
There should be no generators elsewhere, since if so, they must survive since the generators that could possibly kill them all die on an earlier page.
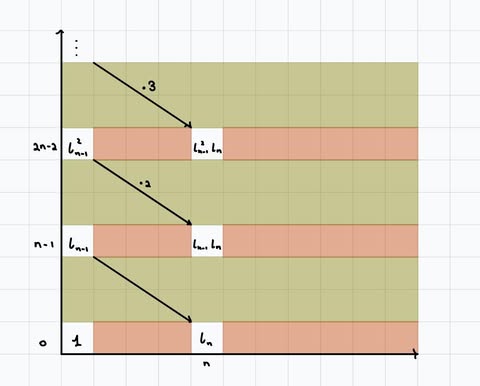
Hence, when \(n\) is odd, the base \(K(\mathbb{Z},n)\) has cohomology \(\mathbb{Q}[\iota_n]/(\iota_n^2)\).
Inductively, we know that for the fiber, \(H^*(K(\mathbb{Z},n-1); \mathbb{Q}) = \mathbb{Q}[\iota_{n-1}]/(\iota_{n-1}^2),\) so on the \(E_2\)-page, we know the \(0\)-th column and also that it has to be \(0\) except the \(0\)-th and the \((n-1)\)-th rows.
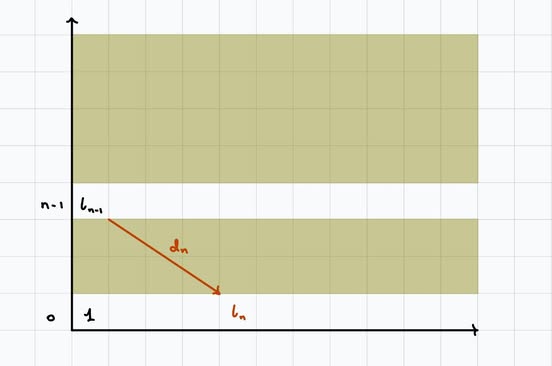
In the \(E_\infty\)-page, the generator \(\iota_{n-1}\) must be killed. The only differential that could kill it is \(d_n\), so there must be a generator in the base in degree \(n\) which \(d_n\) maps to.
This new generator causes there to be an \(\iota_{n-1}\iota_n\) term. But by Leibniz we have \(d_n(\iota_{n-1}\iota_n) = \iota_n^2.\) Inductively we have a \(\iota_{n-1}\iota_n^k\) term, and fortunately Leibniz always gives \(d_n(\iota_{n-1}\iota_n^k) = \iota_{n}^{k+1}.\) So all these terms are killed in the \(E_{\infty}\) page.
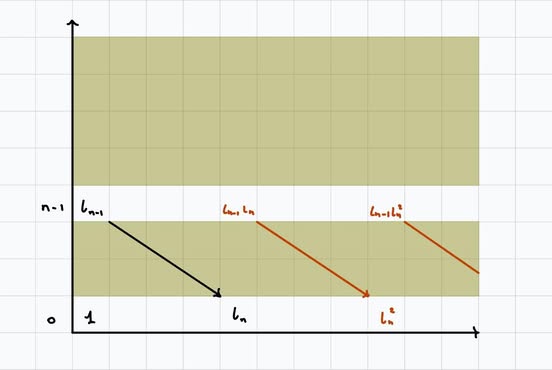
There are no generators elsewhere for degree reasons.
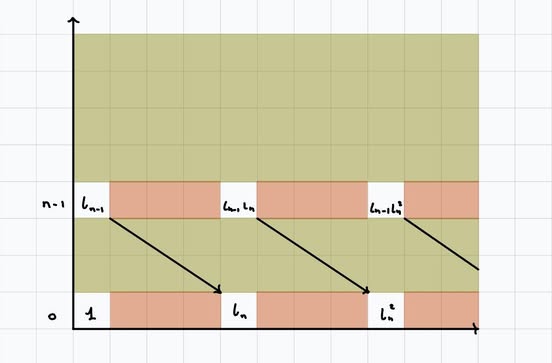
Hence, when \(n\) is even, the base \(K(\mathbb{Z},n)\) has cohomology \(\mathbb{Q}[\iota_n]\).
Following the general strategy, we first apply the Serre spectral sequence to the fibration $$W_{\geq n+1}S^n \hookrightarrow S^n \rightarrow K(\mathbb{Z},n)$$ to find the cohomology of \(W_{\geq n+1}S^n\). This is the same rank as the homology by universal coefficients, and then we apply Hurewicz.
Notice that the map \(S^n \rightarrow K(\mathbb{Z},n)\) is the Hurewicz map which pulls back the generator of \(K(\mathbb{Z},n\)) in the cohomology, so in particular the generator of \(K(\mathbb{Z},n)\) should survive to the \(E_{\infty}\)-page.
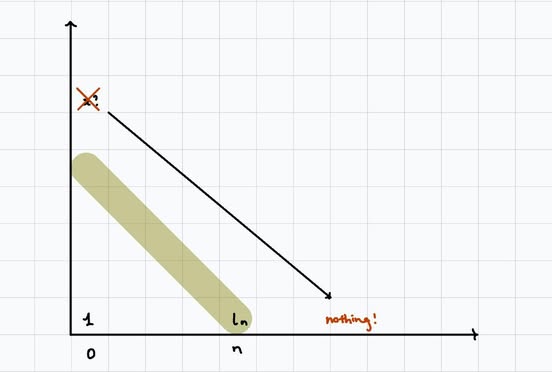
This means that there can't be anything in the cohomology of the fiber \(W_{\geq n+1}S^n\), because there is nothing on the bottom row to kill it. Hence, all of its higher rational homology groups are zero, so all of its higher rational homotopy groups are zero by Hurewicz. But $$\pi_i(W_{\geq n+1}S^n) \otimes \mathbb{Q} = \pi_i(S^n) \otimes \mathbb{Q}$$ for \(i > n\), then it follows that $$\pi_i(S^n) \otimes \mathbb{Q} = 0$$ as desired.
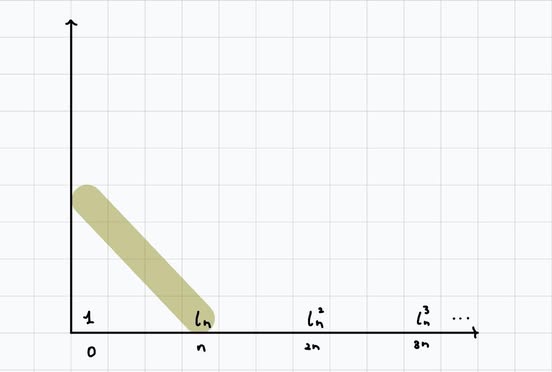 We do want to kill the \(\iota\), so we know that there is a generator in degree \(2n-1\) in the fiber.
We do want to kill the \(\iota\), so we know that there is a generator in degree \(2n-1\) in the fiber.
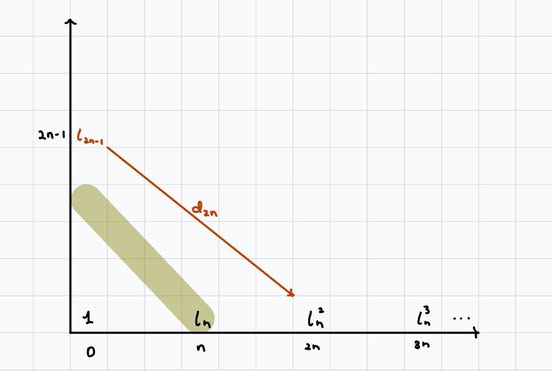 This creates \(\iota_{2n-1}\iota_n^k\), to which we can apply Leibniz to see that \(d_{2n}(\iota_{2n-1}\iota_n^k) = \iota_n^{k+2}.\)
This creates \(\iota_{2n-1}\iota_n^k\), to which we can apply Leibniz to see that \(d_{2n}(\iota_{2n-1}\iota_n^k) = \iota_n^{k+2}.\)
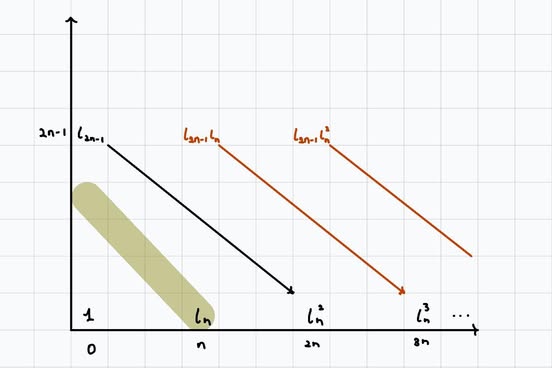 There can't be any other generators for degree reasons.
There can't be any other generators for degree reasons.
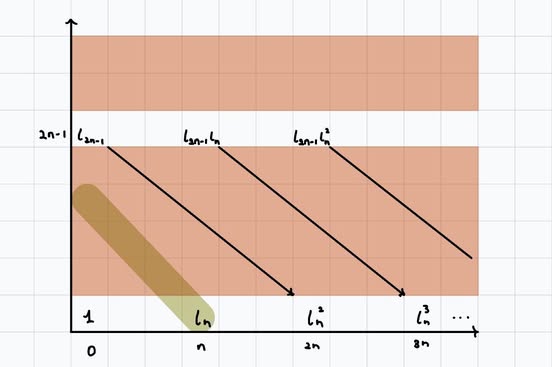 Hence, the cohomology of \(W_{\geq n+1}S^n\) has no generators until degree \(2n-2\). In particular, by general strategy, \(\pi_i(S^n) \otimes \mathbb{Q} = 0\) for \(n< i <2n-1\), since \(\pi_i(W_{\geq n+1}S^n) \otimes \mathbb{Q} = 0\) for \(i < 2n-1\).
Also, we know that
$$\pi_{2n-1}(W_{\geq n+1}S^n) \otimes \mathbb{Q} = \mathbb{Q}$$
which means that there is a copy of \(\mathbb{Z}\) in \(H^{2n-1}(W_{\geq n+1}S^n)\). In particular this means there is a map
$$ W_{\geq n+1}S^n \rightarrow K(\mathbb{Z},2n-1)$$
which pulls back the generator in cohomology.
Now consider the following fibration:
$$ F \hookrightarrow W_{\geq n+1}S^n \rightarrow K(2n-1).$$
Now we can proceed with the exact same argument for the case of odd \(n\) to conclude that the higher homotopy groups are zero. Hence we've shown that
$$\pi_i(S^n) \otimes \mathbb{Q} = \mathbb{Q}$$
for \(i = n, 2n-1\) and zero elsewhere.
Hence, the cohomology of \(W_{\geq n+1}S^n\) has no generators until degree \(2n-2\). In particular, by general strategy, \(\pi_i(S^n) \otimes \mathbb{Q} = 0\) for \(n< i <2n-1\), since \(\pi_i(W_{\geq n+1}S^n) \otimes \mathbb{Q} = 0\) for \(i < 2n-1\).
Also, we know that
$$\pi_{2n-1}(W_{\geq n+1}S^n) \otimes \mathbb{Q} = \mathbb{Q}$$
which means that there is a copy of \(\mathbb{Z}\) in \(H^{2n-1}(W_{\geq n+1}S^n)\). In particular this means there is a map
$$ W_{\geq n+1}S^n \rightarrow K(\mathbb{Z},2n-1)$$
which pulls back the generator in cohomology.
Now consider the following fibration:
$$ F \hookrightarrow W_{\geq n+1}S^n \rightarrow K(2n-1).$$
Now we can proceed with the exact same argument for the case of odd \(n\) to conclude that the higher homotopy groups are zero. Hence we've shown that
$$\pi_i(S^n) \otimes \mathbb{Q} = \mathbb{Q}$$
for \(i = n, 2n-1\) and zero elsewhere.
Now that we've proven that the only free part of \(\pi_i(S^n)\) is in degree \(n\) and in degree \(2n-1\) for even \(n\), we must show that the torsion part is finitely generated. The intuition: if we repeated the whole process with \(\mathbb{Z}\) coefficients, we shouldn't be adding too many generators at each step: if we know finite generation of the fiber and the base, or of the base and the total space, then we should get finite genration for the total space, or for the fiber, respectively.
This two-out-of-three idea is formalized by Serre classes of abelian groups. This is also sometimes called \(\text{mod } \mathcal{C}\) theory.
Definition. A Serre class \(\mathcal{C}\) is a class of abelian groups closed under taking subgroups, quotients, and extensions. Equivalently, for a short exact sequence $$ 0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0$$ of abelian groups, if two of \(\{A,B,C\}\) are in \(\mathcal{C}\), then so is the third.
Examples.
Proposition. Suppose, in addition, that \(\mathcal{C}\) is a Serre class with \(A \otimes B\) and \(\text{Tor}(A,B) \in \mathcal{C}\) if \(A,B \in \mathcal{C}.\) Take a Serre fibration $$F \hookrightarrow E \rightarrow B$$ with path-connected \(B\) and suppose \(\pi_1(B)\) acts trivially on \(H_*(F; \mathbb{Z})\), then if two of $$\tilde{H_*}(F; \mathbb{Z}), \quad \tilde{H_*}(E; \mathbb{Z}), \quad \tilde{H_*}(B; \mathbb{Z})$$ are in \(\mathcal{C}\) then so is the third.
The other two cases go similarly: find the appropriate exact sequence on each page and induct down from the \(E^{\ell}\)-page (for \(\ell >> 0\)) to find that everything is in \(\mathcal{C}\).
One immediate application of this proposition is that the integral cohomology of \(K(\mathbb{Z}/m,n)\) is finitely-generated, inductively from the Lens spaces, using the path-loop fibration. Once we have this, we can do this again with the fibrations coming from the Whitehead tower of \(S^n\) and inductively see that all the homotopy groups should be finitely generated.
Last revised on 03.26.2025.