date: 05.12.2025
I give this talk at a workshop on moduli spaces of pseudoholomorphic curves. This is the first talk on \(\infty\)-categories and it is based on HTT, Kerodon, and nLab. My job is to lay down some definitions and assert some facts.
For a \(1\)-category \(\mathcal{C}\), Yoneda's lemma states that the Yoneda embedding $$j: \mathcal{C} \rightarrow \text{Set}^{\mathcal{C}^{\text{op}}}$$ $$ C \mapsto \text{Hom}_{\mathcal{C}}(-,C)$$ is fully faithful, where \(\text{Set}^{\mathcal{C}^{\text{op}}}\) is the category of set-valued presheaves over \(\mathcal{C}\). In the case of \(\infty\)-categories, the mapping spaces are Kan complexes, so we consider space-valued presheaves.
Definition. Take \(S\) a simplicial set, define \(\mathcal{P}(S)\) the simplicial set \(\text{Fun}(S^{\text{op}}, \textbf{Spc})\) where \(\textbf{Spc} := N(\text{Kan}).\) This is the \(\infty\)-category of presheaves on \(S\).
Functor categories are sometimes opaque; luckily, via straightening-unstraightening, functors in \(\text{Fun}(S^{\text{op}}, \textbf{Spc})\) correspond to right fibrations.
Definition. A morphism \(f:X \rightarrow S\) of simplicial sets is a right fibration if \(f\) has the right lifting property with respect to all inner and right horn inclusions $$\begin{CD} \Lambda_k^n @>>> X \\ @VVV @VVfV \\ \Delta^n @>>> S \end{CD}$$ for \(0 < k \leq n.\)
The vibe for going between presheaves and right fibrations: given a functor to \(\textbf{Spc}\), construct fibration by collecting into "fibers" the target of the functor, and the homotopical information upstairs is given by the homotopical information in the target of the functor. The condition of being a right fibration ensures we land in \(\textbf{Spc}\) and not just \(\text{Cat}_{\infty}.\) Lots of details to check here, you can read more about the straightening-unstraightening equivalence in [these lovely notes] by Rafah Hajjar. (Everything is phrased in terms of cocartesian/left fibrations there, so just take the dual notions.)
Remark. The presheaf category \(\mathcal{P}(S)\) admits small limits and colimits. One explanation of this is that this is true of \(\textbf{Spc}.\)
Yoneda. Let \(S\) be a simplicial set. Then the Yoneda embedding $$j: S \rightarrow \mathcal{P}(S)$$ is fully faithful.
Look [here] to see how the proof goes.
Often, we want to restrict from a bigger category to a smaller one while keeping track of the relevant structure. Classically we do this via adjunctions, with the left adjoint playing the role of the "free" functor and the right adjoint playing the role of the "forgetful" one, and we define it via checking the hom-sets. To define adjunctions \(\infty\)-categorically we want also control over coherence information, and the easiest way to do this is to define it via unit and counit maps.
Definition. For functors of \(\infty\)-categories $$F: \mathcal{C} \leftrightarrows \mathcal{D} : G$$ the pair of natural transformations (i.e. \(2\)-simplices) \(\eta: \text{id}_{\mathcal{C}} \Rightarrow G \circ F\) and \(\epsilon: F \circ G \Rightarrow \text{id}_{\mathcal{D}}\) are compatible up to homotopy if in \(\text{Fun}(\mathcal{C}, \mathcal{D})\) there exists the \(2\)-simplex
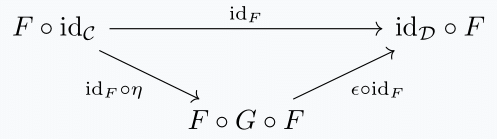
and in \(\text{Fun}(\mathcal{D}, \mathcal{C})\) there exists the \(2\)-simplex
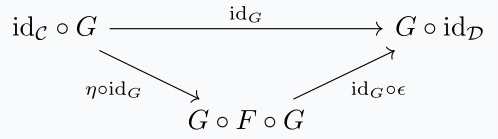
In this situation we say that \(\eta\) is the unit of an adjunction and \(\epsilon\) is the counit. The data of the adjunction between \(F\) and \(G\) is a choice of unit and counit.
Fact. A left adjoint preserves small colimits; a right adjoint preserves small limits. (Just think about where cones/cocones get mapped!) The converse is true with size restrictions on the categories.
Fact. Adjoints are unique up to contractible choice: let \(\text{Fun}^L(\mathcal{C}, \mathcal{D})\), \(\text{Fun}^R(\mathcal{C}, \mathcal{D})\subset \text{Fun}(\mathcal{C}, \mathcal{D})\) denote that sub \(\infty\)-categories of left and right adjoints respectively. Then there is a canonical equivalence of \(\infty\)-categories $$\text{Fun}^L(\mathcal{C}, \mathcal{D}) \xrightarrow{\sim} \text{Fun}^R(\mathcal{D}, \mathcal{C})^{\text{op}}$$ which takes a left adjoint to its corresponding right adjoint.
Uniquness lets us define things in terms of adjunctions; one example is the notion of Kan extensions. Essentially, a left Kan extension fills a left \(2\)-horn in \(\text{Cat}_{\infty}\) and a right Kan extension fills a right \(2\)-horn in \(\text{Cat}_{\infty}\). Note that \(\text{Cat}_{\infty}\) is a Kan complex so that horn fillings always exist. The Kan extension is one such filling which is universal in the following sense.
Definition. Fix \(p: \mathcal{C} \rightarrow \mathcal{C'}\); this induces $$p^*: \text{Fun}(\mathcal{C}, \mathcal{D}) \rightarrow \text{Fun}(\mathcal{C'}, \mathcal{D}).$$ Its left adjoint, if exists, is the left Kan extension. Similarly, its right adjoint, if exists, is the right Kan extension.
They exist barring size issues. Left Kan extensions preserve colimits and right Kan extensions preserve limits.
We might want to consider subcategories which "capture their own structures entirely" in the bigger category. These are the reflective subcategories.
Definition. A reflective subcategory is a subcategory for which the inclusion functor has a left adjoint.
Suppose we are given an adjunction $$F: \mathcal{C} \leftrightarrows \mathcal{D} : G$$ and \(\mathcal{A}\), \(\mathcal{B}\) reflective subcategories of \(\mathcal{C},\mathcal{D}\) respectively. If \(F(\mathcal{A})\subseteq \mathcal{B}\) or \(G(\mathcal{B})\subseteq \mathcal{A}\), then \(F,G\) restrict to an adjunction on \(\mathcal{A},\mathcal{B}.\)
One example of a reflective subcategory: the category of sheaves over \(S\), \(\mathcal{Sh}(S)\), inside \(\mathcal{P}(S)\). We first define sheaves over topological spaces.
Definition. A sheaf \(\mathcal{F}\) over a topological space \(X\) is a presheaf $$\mathcal{F}: \text{Open}(X)^{\text{op}} \rightarrow \textbf{Spc}$$ such that for any open cover \(\{U_i\}\) of \(U\), we have $$\mathcal{F}(U) \rightarrow \prod_i \mathcal{F}(U_i) \rightrightarrows \prod_{i,j} \mathcal{F}(U_i \cap U_j) \substack{\rightarrow\\[-2em] \rightarrow \\[-2em] \rightarrow} \cdots$$
(The definition of a sheaf only required a sense of covering, to make sense of gluing. We can generalize the notion of a sheaf to be over any categories with a reasonable notion of covering, not just categories of open sets, i.e. Grothendieck topology.)
Definition. The sheafification functor is the left adjoint to the inclusion functor \(\mathcal{Sh}(S) \hookrightarrow \mathcal{P}(S).\)
The pushforward-pullback adjunction of presheaves gives one example of passing adjunctions to a reflective subcategory.Definition. Given a map of topological spaces \(f: X \rightarrow Y,\) the pushforward functor $$f_*: \mathcal{Sh}(X) \rightarrow \mathcal{Sh}(Y)$$ is defined by $$(f_*\mathcal{F})(U) := \mathcal{F}(f^{-1}(U))$$ which sends sheaves to sheaves. Its left adjoint, the pullback functor, $$f^*: \mathcal{Sh}(Y) \rightarrow \mathcal{Sh}(X)$$ can be constructed as presheaf pullback \(U \mapsto \text{colim}_{f(U) \subset V} \mathcal{F}(V)\) composed with sheafification.
Notice that the discussion in this section could've been done over presheaves and sheaves valued in arbitrary \(\infty\)-categories and not just in \(\textbf{Spc}.\)
For an arbitrary \(\infty\)-category \(\mathcal{C}\), it is rare for it to admit small colimits. It is always possible, however, to embed it into a larger \(\infty\)-category \(\hat{\mathcal{C}}\) which does admit small colimits. The cocompletion is the universal such category.
Definition. Let \(h: \mathcal{C} \rightarrow \hat{\mathcal{C}}\) be a map of \(\infty\)-categories; we say that \(\hat{\mathcal{C}} \) is a cocompletion of \(\mathcal{C}\) if
Theorem. The Yoneda embedding $$j: S \rightarrow \mathcal{P}(S)$$ is a cocompletion.
Last revised on 05.12.2025.