date: 02.17.2025
I give this talk as part of a reading seminar on Markus Land's Introduction to Infinity-Categories. I'm meant to cover sections 2.4: Localizations and 2.5: Fat Joins, Fat Slices and Mapping Spaces. These notes follow the book somewhat loosely, and prioritize constructions over proofs.
In the first part of this talk, I define localizations via a universal property, show that it is unique, and construct it. I also give some key examples. In the second part of the talk, I consider different, equivalent models for the mapping space between two objects in an \(\infty-\)category. Thirdly, I give the definition of the homotopy-coherent nerve. Each part is self-contained.
Notation: \(\mathcal{C}, \mathcal{D}\) are \(\infty-\)categories, \(S \subseteq \mathcal{C}_1\) a subset of morphisms of \(\mathcal{C}\).
Just like for \(1-\)categories, the idea of localization for an \(\infty-\)category is to declare certain morphisms equivalences by adding their inverses. We define this via taking the universal object to the property of sending the desired morphisms to equivalences. To make this definition precise, take notation \(\text{Fun}^{S}(\mathcal{C},\mathcal{D})\) to mean the \(\infty\)-category of functors from \(\mathcal{C}\) to \(\mathcal{D}\) which send morphisms in \(S\) to equivalences in \(\mathcal{D}.\)
Definition. A functor \(i: \mathcal{C} \rightarrow \mathcal{C}[S^{-1}]\) of \(\infty\)-categories is a Dwyer-Kan localization of \(\mathcal{C}\) along \(S\) if, for any \(\mathcal{D}\), the functor $$i^*: \text{Fun}(\mathcal{C}[S^{-1}], \mathcal{D}) \rightarrow \text{Fun}(\mathcal{C},\mathcal{D})$$ factors through a Joyal equivalence to \(\text{Fun}^S(\mathcal{C},\mathcal{D})\):
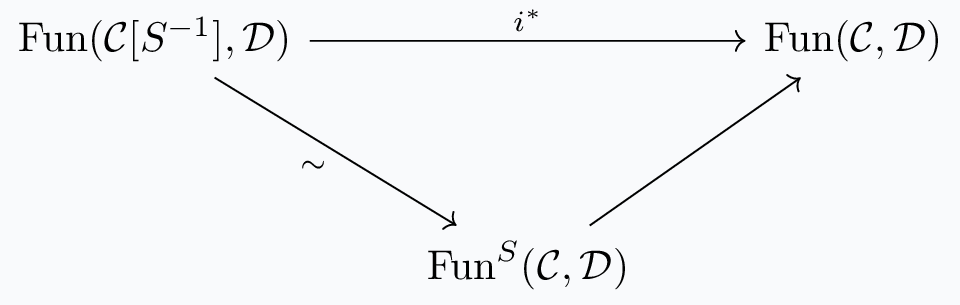
Recall that a functor of \(\infty\)-categories is a Joyal equivalence if it is an equivalence as a morphism in \(\text{Cat}_{\infty}\); last time, we've seen that a functor being a Joyal equivalence is the same thing as being fully faithful and essentially surjective.
As with all objects defined via universal properties, we must check existence and uniqueness. Uniqueness is easier, so we do this first.
Suppose we have two localizations of \(\mathcal{C}\) along \(S\), \(i: \mathcal{C} \rightarrow A\) and \(j: \mathcal{C} \rightarrow B\). We prove the following triangle
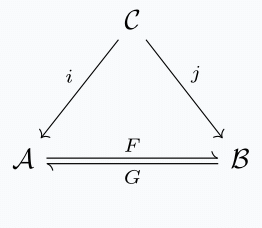exists and commutes, with \(F,G\) being Joyal equivalences. To get \(G\), consider the following diagram:
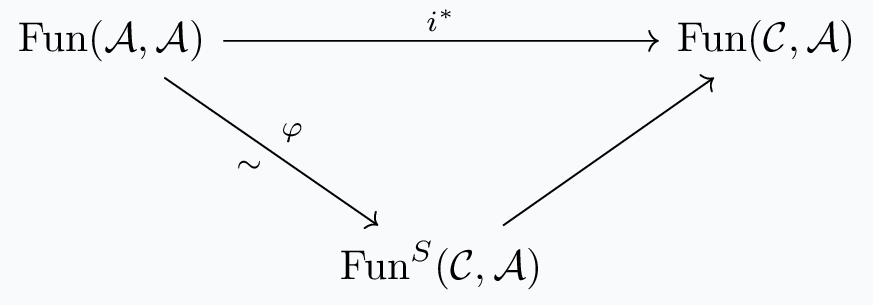
Notice that here, \(i^*(\text{id}_A) = i\). Take \(g \in \text{Fun}^S(\mathcal{C}, \mathcal{A})\) to be \(g = \varphi(\text{id}_A)\). Now consider the diagram
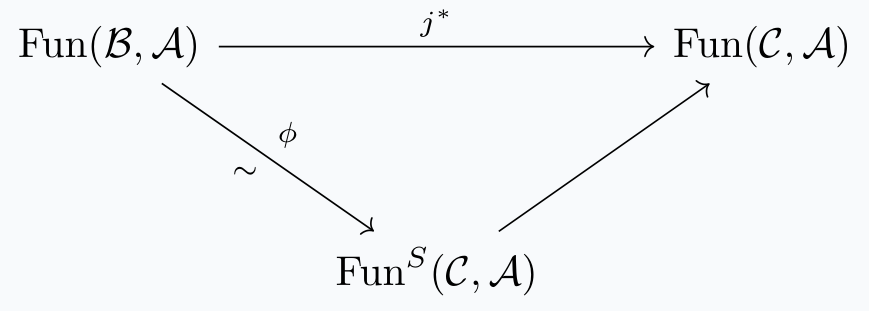
and now take \(G = \phi^{-1}(g)\). The fact that \(Gj\simeq i\) follows from the fact that \(g\) is mapped to \(i\) in the first triangle and to \(Gj\) in the second. We can construct \(F\) completely analogously. (Notice this construction also makes clear how the definition is in fact a universal property.)
Now it suffices to show that \(GF \simeq \text{id}_A\) and \(FG \simeq \text{id}_B\). Notice, in the first triangle, that \(i^*\) is the composition of two fully faithful functors, so it suffices show that the images of \(GF\) and \(\text{id}_A\) under \(i^*\) are equivalent. And indeed they are: $$GFi \simeq Gj \simeq i$$ and similarly $$FGj \simeq Fi \simeq j.$$
We have the factorization $$\text{Fun}(J, \mathcal{D}) \rightarrow \text{Fun}^{(\Delta^1)_1}(\Delta^1, \mathcal{D}) \hookrightarrow \text{Fun}(\Delta^1, \mathcal{D}).$$ We need to show that the first map is a Joyal equivalence. Last time, we noted that trivial Kan fibrations are Joyal equivalences. In the book, the proof of Lemma 2.4.5 shows that this map is a trivial Kan fibration via giving a filtration of \(J\).
Consider the pushout
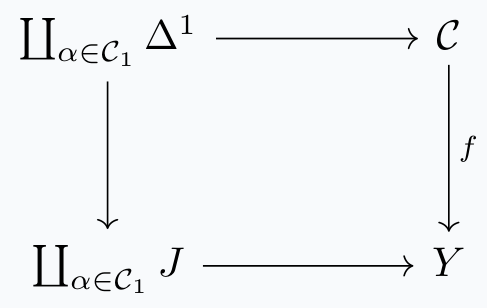and factor \(Y \rightarrow *\) as an inner anodyne map \(g: Y \rightarrow X\) followed by an inner fibration. Take \(gf: \mathcal{C} \rightarrow X\) to be the desired map; for proof see Lemma 2.4.6 of the book.
Let \(\mathcal{C}_S\) be the smallest \(\infty-\)subcategory of \(\mathcal{C}\) which contains \(S\). Consider the following pushout
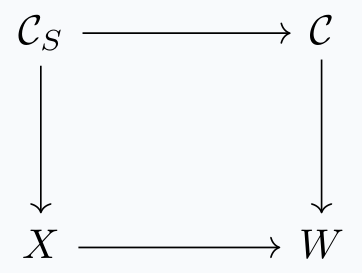where \(C_S \rightarrow X\) is the localization defined in the previous step. Take \(f: \mathcal{C} \rightarrow W\) to be the desired map; for proof see Lemma 2.4.8 of the book.
Notation: \(S, X, Y\) simplicial sets, \(\mathcal{C}\) an \(\infty\)-category, and \(a,b \in \text{Ob}(\mathcal{C}).\)
Previously, we've glossed over what a mapping space \(\text{map}_{\mathcal{C}}(a,b)\) is. As a set, it is the subset of \(\mathcal{C}\) which has source \(a\) and target \(b\). It is then reasonable to define the mapping space as the following pullback:
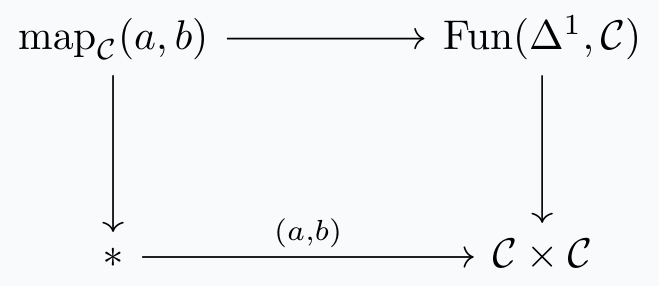
(This diagram lives in \(\text{sSet}\); it is a theorem that the mapping space is actually a Kan complex and therefore a space.) This definition parameterizes the mapping space over both the source and the target. We may also define it in a way where it is parameterized over just the source, or just the target. To do this, we will need a notion of "all the maps to \(b\)", denoted \(\mathcal{C}_{/b}\), or a notion of all the maps from \(a\)", denoted \(\mathcal{C}_{/a}\). (These are called slice categories which we will define shortly.) Once we have these notions, we can define the right mapping space as the pullback
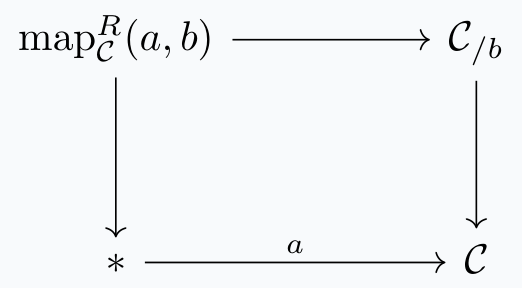
and the left mapping space as the pullback
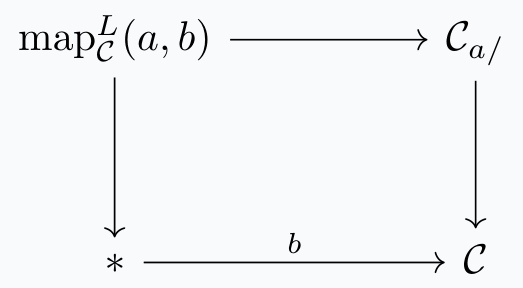We will show that in fact, all three definitions are homotopy equivalent. But first, we need to define slice categories.
Last time, we saw the definition for joins of categories. Let's now define it for simplicial sets. For a linearly ordered set \(J\), a cut of \(J\) is a decomposition \(J = J_1 \coprod J_2\) such that \(j_1 < j_2\) for \(j_i \in J_i.\)
Definition. The join \(X \star Y\) sends, for a finite linear ordered set \(J\), $$(X \star Y)(J) = \coprod_{(J_1,J_2 \in \text{cut}(J))} X(J_1) \times Y(J_2).$$
Definition. For \(p:S \rightarrow X\), the slice category \(X_{p/}\) as a simplicial set is $$[n] \rightarrow \text{Hom}_{\text{sSet}_{S}}(S \star \Delta^n, X)$$ and \(X_{/p}\) as a simplicial set is $$[n] \rightarrow \text{Hom}_{\text{sSet}_{S}}(\Delta^n \star S, X).$$
Note. The functor $$(-)_{p/}: \text{sSet}_{S/} \rightarrow \text{sSet}$$ $$(p:S \rightarrow X) \mapsto X_{p/}$$ is the right adjoint to \(S \star -: \text{sSet} \rightarrow \text{sSet}_{S/}\), and \((-)_{/p}\) is right adjoint to \(- \star S\).
You may object that the definition of a join is too constructive, and instead use the following pushout as definition.
Definition. The pushout \(X \diamond Y\) of the diagram
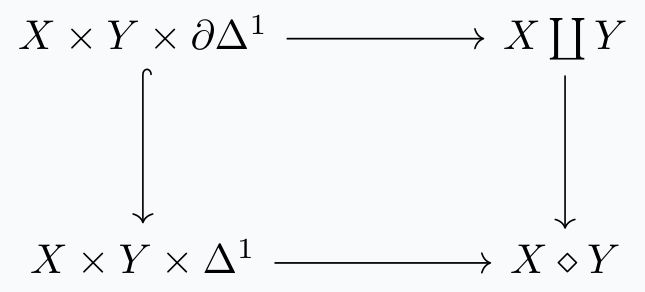
is the fat join of \(X\) and \(Y\).
Theorem. The join \(X \star Y\) and the fat join \(X \diamond Y\) are Joyal equivalent.
The proof of this can be found in section 2.5 of the book.
We can also define fat slices using this definition of joins, by replacing each instance of a join in the definition of slice by a fat join.
Definition. For \(p:S \rightarrow X\), the fat slice \(X^{p/}\) is $$[n] \rightarrow \text{Hom}_{\text{sSet}_{S}}(S \diamond \Delta^n, X)$$ and \(X^{/p}\) is $$[n] \rightarrow \text{Hom}_{\text{sSet}_{S}}(\Delta^n \diamond S, X).$$
Note. The slices \(X_{p/}, X_{/p}\) are respectively Joyal equivalent to fat slices \(X^{p/}, X^{/p}\), and similar to the adjunction between joins and slices, there is an adjunction between fat joins and fat slices.
As it turns out, the mapping space \(\text{map}_{\mathcal{C}}(a,b)\) also arises as the following pullbacks:
comparing this with the pullback squares of the definition of the left and right mapping spaces using the Joyal equivalence map between slices and fat slices gives the desired equivalence. You can find more details in the book, in section 2.5.
I define this here because it is important and missed previously. The homotopy-coherent nerve (also known as the simplicial nerve) is a functor $$N:\text{Cat}_{\Delta} \rightarrow \text{sSet}$$ on simplicially-enriched categories which agrees with the classical nerve on \(1-\)categories. The point of this is that the simplicially-enriched categories come with the information of homotopies, and we want to capture that in the nerve. (Recall that the classical nerve doesn't have this information since \(n-\)compositions are unique for \(1-\)categories.)
To define it, we need a simplicially-enriched version of \(\Delta^n\). If \(J\) is a linearly ordered set and \(i,j \in J\), let \(P_{i,j}\) be a poset consisting of subsets of \([i,j] \subset J\), partially ordered by inclusion.
Definition. The simplicially-enriched category \(\mathfrak{C}[\Delta^J]\) has objects given by elements of \(J\) and $$\text{Hom}_{\mathfrak{C}[\Delta^J]}(i,j) = \begin{cases} \varnothing & i > j \\ N(P_{i,j}) & i \leq j.\end{cases}$$
Now, for any simplicially-enriched category \(\mathcal{C}\), define its homotopy-coherent nerve \(N(\mathcal{C})\) as the simplicial set where $$N(\mathcal{C})_n = \text{Hom}_{\text{Cat}_{\Delta}}(\mathfrak{C}[\Delta^n], \mathcal{C}).$$
Details are in section 1.2 of the book.
Last revised on 02.17.2025.